This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
OK, the title might need some explaining: Both tasks this week have us looking through lists of numbers and doubling some of them.
Task 1 › Double Exist
Task 1’s premise is simple enough: we take in a list of @ints and return a true value if the list contains a number and its double.
We also have the restriction that the same list element cannot be its own double. Zero is the only integer this can happen with. For example, (0) returns false even though 2×0 = 0, but (0,0) returns true because the second zero is a different list element.
We can solve this in O(n) time with a little bit of housekeeping: we will track whether we have seen the double of a number, and the half of a number (if that number is even). Tracking both doubles and halves ensures that we will find the 2k whether it comes before or after k in the list.
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
Task 1 – 3rd Maximum
Task 1 this week is to take a list of integers and find the 3rd unique maximum value, or if there are fewer than 3 unique values, return the overall maximum. Examples:
Integers
3rd Maximum
5, 6, 4, 1
4
4, 5
5
1, 2, 2, 3
1
To accomplish this, I just sort the input integers and get the uniq list from that (from core module List::Util). The sort is O(n log n), but it’s only done once, so that’s our overall complexity.
It would also be possible to use a sliding window for this, but then every insert would be more expensive, up to O(wn) complexity where w is the window size. For constant w where w << n, this might be a win, but Perl’s slow looping speed might make that constant factor dominate, and the code would have been more complex. Still, it could have been fun to experiment with some profiling, given more time.
The general case solution is extremely simple:
sub nth_max {
my $n = shift;
my @uniq_sorted = uniq sort { $b <=> $a } @_;
$uniq_sorted[ @uniq_sorted >= $n ? $n - 1 : 0 ]
}
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
The first challenge this week has us finding the count of words that appears exactly once in each of two lists. For example:
('Perl', 'is', 'my', 'friend'), ('Perl', 'and', 'Raku', 'are', 'friend') Should return 2 since Perl and friend appear once in each list. But,
('twice', 'twice'), ('twice') should return 0, since twice appears more than once in one of the arrays.
Since it was easy, I opted to support an arbitrary number of arrays instead of just two. It would of course be trivial to limit the input to two arrays. I also support scalar and list context, so you can easily get just the count (as the task asks), or call the function in list context to get the actual list of common words.
Since my algorithm is O(n), I do not return sorted results by default, as a minor optimization. If stable output is needed, simply sort the result.
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
I thought I’d take the rare (for me) step of implementing this week’s challenges in Python as well as Perl.
Happy Canada Day!
Task 1 – Complete Day
The first task has us look through a list of hours and count the number of pairs that add up to a multiple of 24.
Perl
My first version was done in a compact functional style, which may be more challenging for Perl novices:
Reading from bottom up as usual, we iterate through the indices of @_ (our hours array) and map { ... } each index to a list of array refs from index to end of list. So, given (1, 2, 3, 4, 5), we would expect to get the following list for this intermediate step:
The first map { ... } then splits this into $m, with the rest of the values in @$_ (note the shift). $m and @$_ are effectively car and cdr if you recall your lisp (although not many of us still do, I suppose).
There is an inner map { ... } that then adds $m to every value in @$_, and maps to 1 if it is a multiple of 24 and 0 if it is not. sum0 from the core module List::Util simply adds them all up to get a count.
More readable example
A more readable version is as follows:
sub complete_day {
my $count = 0;
while (my $m = shift) {
$count += sum0 map { ($m + $_) % 24 == 0 } @_
}
$count
}
This one simply maintains a $count as it goes, peeling off a new $m each time through the while() { ... } loop, with a similar inner map { ... } as before.
For Perl Weekly Challenge code, I like to show off some different programming styles. Which one I would actually use in production is another question entirely.
Python
I didn’t think too hard about this one:
def complete_day(hours):
count = 0
for i, m in enumerate(hours):
for n in filter(lambda n: ((m + n) % 24 == 0), hours[i+1:]):
count += 1
return(count)
This works similarly to the second Perl example.
Task 2 – Maximum Frequency
The second task this week has us looking at a list of values, finding the maximum frequency of any particular value, and then returning the total number of items with that maximum frequency. This is best demonstrated by example.
Given (1, 2, 2, 4, 1, 5), both 1 and 2 occur twice, so the maximum frequency is 2. Since there are two different values with that frequency, we would return 2 x 2 = 4.
Given (1, 2, 2, 4, 6, 1, 5, 6), 1, 2, and 6 occur twice, so the maximum frequency is 2, but now there are three different values with that frequency, so we return 3 x 2 = 6.
Perl
sub max_freq {
my %freq; # Frequency table
$freq{$_}++ for @_;
my $max_freq = max values %freq; # Maximal frequency
$max_freq * grep { $_ == $max_freq } values %freq;
}
There are three essential steps here. First, we build a %frequency table, mapping values to the number of times they appear. Then we find the $max_freq with a quick pass through the values of that hash.
The final answer is generated by multiplying $max_freq by the count of values where the frequency is equal to $max_freq. Easy!
Python
def max_freq(ints):
# Annoying special case for empty list
if len(ints) == 0:
return(0)
# Build the frequency table (freq[n] = # of times n is in ints)
freq = {}
for n in ints: freq[n] = freq.setdefault(n,0) + 1
max_freq = max(freq.values()) # Maximal frequency
return(sum(filter(lambda x: x == max_freq, freq.values())))
This roughly follows the Perl code, although we need a special case for empty lists (otherwise we get an error).
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
This week’s tasks have a little bit more meat on their bones, which I quite enjoyed. They are user-submitted, as well, and it’s always fun to see what people come up with when submitting tasks.
Task 1 – Banking Day Offset
This task comes from the mind of Lee Johnson. Here, we’re given the following inputs:
Number of days [$offset]
Start date [$start_date]
List of dates which are holidays (optional) [@holidays]
From that, we’re supposed to return the date that is $offset working days from the $start_date, ignoring weekends and @holidays. This is straightforward. I opted to use the core Perl module Time::Piece to get the day of the week. There are about n + 1 different ways to do that, though.
The function starts with some initialization:
sub bank_holiday_ofs {
my ($start_date, $offset, @holidays) = @_;
my $t = Time::Piece->strptime($start_date => $date_fmt) - 86400;
my %holiday = map { $_ => 1 } @holidays;
$offset++; # Account for today
The %holiday hash simply maps the dates to a true value so $holiday{$date} will be true iff$date is in @holidays. The $offset variable gets an extra kick to account for the current day.
From here, we loop until $offset is zero:
while ($offset) {
$t += 86400; # Advance day
$offset-- unless $t->wday == 1 or $t->wday == 7
or $holiday{ $t->strftime($date_fmt) };
}
From years of frequent use, 86,400 has sufficient semantic meaning as “1 day” that I’m not bothered about the naughty magic number. If that’s not your style, Time::Seconds has a ONE_DAY constant.
The loop is simple. Add a day, and then subtract a day from $offset unless it’s a weekend or holiday.
We are also required to handle escaped quotes (\") and (optionally) multiline tags. I wrote a pure-Perl parser that handles all of this. It’s easiest to think of in two parts:
Top level line parser
This is the part that takes in a line of text and decides what to do with it. First, let’s define our $Open and $Close tags:
my ($O, $C) = (qr/^\s*\{\%\s*/, qr/\s*\%\}\s*$/); # Tokens gobble whitespace
I could have just done a simple {% and %} set, but I wanted to allow optional whitespace. A recurring theme you’ll see with my solution (and my parsers in general) is that I tend to be permissive with inputs, but precise with outputs.
Now I loop through each line of input (in this case, the __DATA__ block):
for (<DATA>) {
chomp;
if ($id) {
if (/${O}end$id${C}/) {
$id{$id}{text} = @text > 1 ? [ @text ] : $text[0];
@text = ();
$id = undef;
} else {
push @text, $_
}
}
elsif (/${O}(?<id>\w+)\s+(?<fields>.+?)${C}/) {
die "No end token found for <$id>" if $id and @text;
$id = $+{id};
die "Duplicate id <$id>" if exists $id{$id};
$id{$id} = { name => $id, fields => parse_fields($+{fields}) };
}
else {
die "Invalid line: <$_>";
}
}
The way this loop works is, if $id is defined, we’ve already seen an open {% tag and we’re expecting either a line of text, or the {% endid %} closing tag, so we look for those and handle them accordingly.
Otherwise, we expect to see a single line {% id key=value, ... %} record or the start of a multi-line record, so we look for that. We pass the key/value portion of the record to the parse_fields() sub, which we’ll look at next.
parse_fields(): The key/value (kv) parser
It might seem like parsing keys and values would be the easy part, and if not for Gabor’s requirement to handle escaped quotes, it might have been. There are several ways I could have tackled this, from tricky eval()s to full-blown grammars, but for my purposes here (and because I felt like it), I decided to implement a simple state machine.
Finite state machines can be described by a directed graph whose vertices contain the possible states the system can be in, and edges are the possible state transitions. To parse the kv pairs as described by this task, the following state machine will do the trick:
State diagram for parsing key/value pairs.
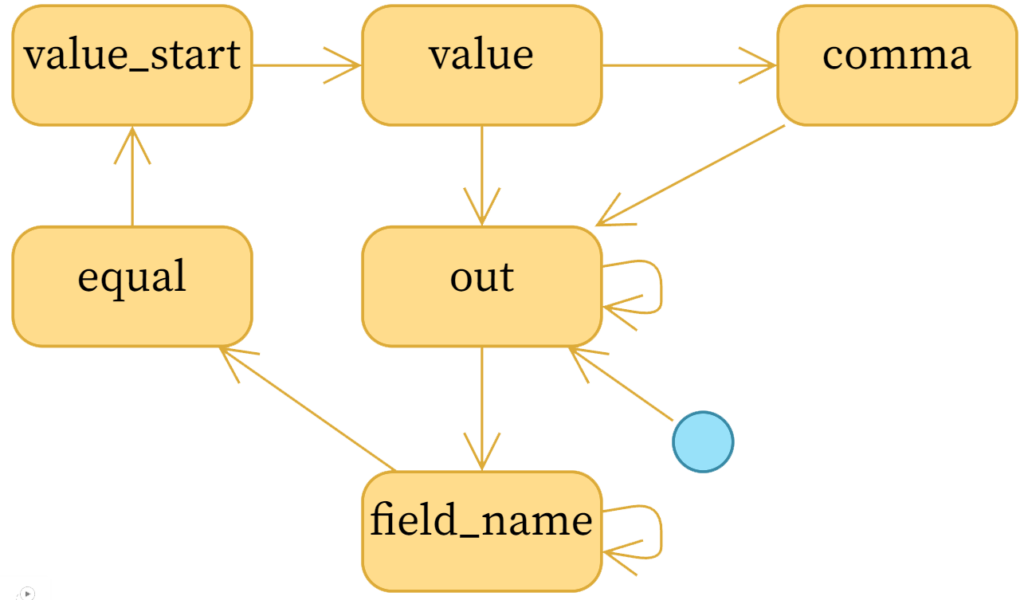
Note: To avoid a cluttered diagram, I’ve omitted arrows on most states that point to themselves, except for field_name and out. It so happens that every state in this particular system can have itself as the next state.
We effectively start from the out state, meaning we are outside of a key/value pair and are waiting for the start of the next key name. Once we see a word character (\w), we go to the field_name state and stay there until we’ve gobbled up all of the \w characters, and then we look for an equal sign. We similarly trundle through the states to find the start of the value (value_start), the value itself, then a comma, and back to out for the next field. We can stop at any time.
One way to implement simple state machines is by simply having a $state variable that you set to the name of the state you’re in, and an if ... elsif ... chain to handle the state transitions. For more complicated, or dynamic state machines, you might reach for one of the many CPAN modules for finite state machines (FSM). But I wanted to show you how it can be done without any help.
My parse_fields() function iterates over the input string character by character. First, we have some top level variables to keep track of:
my %fields;
my $state = 'out'; # Outside of KV pair
my $backslash = 0; # Substate for whether we're backslashed
my $name = undef; # Field name
my $value = undef; # Field value
my $expected_closing_quote; # If defined, value must end with this
Our output will be %fields. The $backslash variable actually captures a parallel state of whether the last character was a backslash (1), whether the current character was escaped (2), or whether neither of those things is true (0). I might have used named values instead, but this made sufficient sense to me.
I decided values could be optionally quoted, by single ('), double (") or nothing, but that the closing quote had to match the opening quote. So that’s what $expected_closing_quote keeps track of.
I do use eval here, but you’ll note it’s done in a safe manner, as I only ever pass two characters to eval, and the first character is a backslash. I could have built up my own hash of slash characters, but that would be error prone and require updating with the language.
If the current character is a backslash, we just set $backslash and go to the next character. If the previous character was a backslash, we do the eval to get the unescaped character. We then set $backslash to 2, which is used when we’re looking for quotes, to avoid ending the value on an escaped quote.
Here’s what a typical state handler looks like:
# Handle the value, with optional quotes and escape sequences
elsif ($state eq 'value_start') {
next if /\s/;
if (/['"]/ and not $backslash) {
$expected_closing_quote = $_;
$state = 'value';
$value = '';
next;
}
$value = $_;
$state = 'value';
}
That is the value state. You’ll see that has the logic I just talked about; if we see our $expected_closing_quote and it wasn’t $backslashed, or we see whitespace and the value is not quoted at all, we have reached the end of the value. So we set $fields{$name} = $value (that’s now part of our return value), set our next state to comma, and go to the next character.
On the other hand, if none of those conditions were true, that means we’re still inside the value, so we append the character to $value and continue. (The value state points to itself.)
I won’t show all of the states here, as the above should give you the flavor of it, but of course you can see my full solution here.
All in all, it’s decently robust for a PWC task solution, but a production version could certainly use some better error checking and reporting. Invalid inputs are mostly handled fairly gracefully, but the resulting output might be confusing.
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
Yes, it’s been a long while! Many a curveball has been thrown at my face. This week’s tasks are pretty quick and easy, so let’s dive right in.
Count Even Digits Number
The first task is simple. Given a list of integers, return the count of integers that have an even number of digits. So, for example, (10, 1, 111, 24, 1000) has 3 values with an even number of digits.
I was in a regex-y mood, so here’s what I came up with (Perl):
sub even_re { ()= "@_" =~ /\b(\d\d)+\b/g }
The pattern is simple: match two digits (\d\d) one or more times (+), separated by a word boundary (\b). That is matched against "@_", which interpolates to the list, separated by $".
Since we use the /g (global) match, we get all matches back. The ()= pseudo-operator turns that into the count of matches. If that were being assigned to a variable, you’d see it written like this instead:
$result =()= $var =~ /pattern/g
Raku
In Raku, I decided to do the slightly more sane thing and grep the list rather than interpolating first:
sub even_re { +@_.grep(/^(\d\d)+$/) }
Without the +, we would return the list of matches. The + forces it to a scalar, giving us the count of matches instead.
Sum of Values
Task 2 has us take in a list of integers and a number $k, and add up the integers whose index in the array contain $k ones. So, for example, given $k = 1 and @ints = (2, 5, 9, 11, 3), we have to look at the binary representation of the array indicies:
Index [base10]
Index [base2]
Value
0
0
2
1
1
5
2
10
9
3
11
11
4
100
3
@ints with index (decimal and binary)
The bold rows (values: 5, 9, 3) have a base-2 index containing only one 1, so the result is 17. Why anyone would want to do this, I couldn’t tell you.
Still feeling a slight bit of regex fever, I based my second task solution around a very simple /1/g regex for counting the 1s in the binary representation of a number. Here’s the full solution:
use List::Util qw< sum >;
sub sum_idx_bit_set {
my $k = pop;
sum map { $_[$_] } grep { $k == ( ()= sprintf('%b',$_) =~ /1/g ) } 0..$#_
}
The whole thing is a grep over all of the indices for any where the binary representation contains $k ones. Those indices are fed into a simple map to get the list element, and the whole thing is sum()med up.
Raku
The Raku solution is conceptually similar, but there are a few language differences:
sub sum_idx_bit_set($k, @n) {
@n[ @n.keys.grep({ (TR:d/10/1/ with .base(2)) == $k }) ].sum
}
I decided to use TR// here, which I could have also done with Perl. Converting to binary is easier in Raku thanks to the base() method. The grep({...}) over the indices of @n sets us up to take a slice of @n and sum() it up.
This solution feels a bit less Raku-ish to me, although my Raku is very rusty at the moment, not having looked at Raku code for nearly two years. Time to get hacking, eh!
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
This week’s tasks include a simple number theory calculation, and a language feature. Here’s a look at task 1.
Odd Abundant Numbers
Abundant numbers are numbers where the sum of the proper divisors is greater than the number. The first odd abundant number is 945. 945’s proper divisors are 1, 3, 5, 7, 9, 15, 21, 27, 35, 45, 63, 105, 135, 189, and 315. (Recall that we exclude 945 itself as a proper divisor.)
The sum of those divisors is 975, so therefore 945 is an abundant number.
Equivalently, a number is abundant if the sum of all divisors is greater than twice the number. We’ll see both variations in the solutions below.
I’m going to take you through a few different approaches. Since I don’t like repeating myself, let’s get some foreshadowing for task #2 going, by using a first class function:
sub n_odd_abundant(&$) {
my ($is_abundant, $N) = @_;
my @r;
for (my $n = 3; $N; $n += 2) {
if ($is_abundant->($n)) {
push @r, $n;
$N--
}
}
@r;
}
The above code takes in a code ref ($is_abundant) and a limit ($N). We loop over all odd numbers, pushing any that pass the $is_abundant check to our result.
Although the above version suited my purposes better, it’s also possible to do this with an iterator, to avoid having to store the intermediate result:
sub odd_abundant_iterator(&) {
my $is_abundant = shift;
my $n = 1;
sub {
do { $n += 2 } until $is_abundant->($n);
$n;
}
}
Now that we have a framework for gathering abundant numbers, let’s try it a few different ways.
Brute force
The first way you might think to try is simply to brute force your way through every divisor of every number. This is O(n) for each number, and takes over a second to find the first 20 numbers:
sub n_abundant_naive {
n_odd_abundant {
my $n = shift;
$n < sum grep { $n % $_ == 0 } 1..$n/2;
} $_[0];
}
Using sqrt
Stopping at \(\sqrt{n} \) perhaps unsurprisingly brings the asymptotic time down to O(\(\sqrt{n} \)). Since divisors come in pairs, we can simply calculate the other divisor and avoid looping through most of the numbers:
sub n_abundant_sqrt {
n_odd_abundant {
my $n = shift;
my $sqrt = sqrt($n);
my $sum = sum map { $_, $n / $_ }
grep { $n % $_ == 0 } 1..$sqrt;
$sum -= $sqrt if $sqrt == int $sqrt;
2*$n < $sum;
} $_[0];
}
It might not seem like a huge change, but the above code runs about 27 times faster than the naïve version, when asked to find the first 20 odd abundant numbers.
Using Math::Prime::Utildivisor_sum
Just for fun, our old friend, Math::Prime::Util has a function that seems perfect for our needs: divisor_sum. It does what it says on the tin: it calculates the sum of the divisors of whatever number we give it.
sub n_abundant_mpu {
n_odd_abundant {
my $n = shift;
my $sum = divisor_sum($n);
2*$n < $sum;
} $_[0];
}
This one is another 12 times faster than the sqrt solution, and 356 times faster than the naïve method. Great, right? Well, not so fast. Under the hood, the divisor_sum function is still finding all divisors for every number, so we’re still at \(O(n \sqrt{n}) \) time. It’s only faster because of the very tightly optimized C code under the hood.
Sieve
We can still do quite a bit better by realizing that since we’re looking for a whole bunch of abundant numbers, we’re repeating the same calculations over and over again, for every multiple of a number we’ve seen already. So as long as we’re willing to tweak the requirement slightly to find all abundant numbers below a given limit (although we’ll see how we can still accommodate the old calling syntax if we really want to), we can do much better:
sub n_abundant_sieve {
my $lim = shift;
my @r;
my @div_sum; # Sum of divisors for each number
for my $n (1..$lim) {
$div_sum[$n*$_] += $n for 1..$lim/$n+1;
push @r, $n if $n % 2 and 2*$n <= $div_sum[$n];
}
@r;
}
When called as n_odd_abundant_sieve(10000), this returns the first 23 odd abundant numbers, about twice as fast as the sqrt version returns 20. That’s because this algorithm runs in \(O(n \log{n}) \) time, which is strictly less than \(O(n \sqrt{n}) \) time for all \(n > 0 \). It grows significantly slower.
Sneaking up on the limit
In number theory circles, finding all numbers below a limit is usually just fine, but if we wanted to be a stickler for the parameters of the challenge and return only the first 20, we could simply call n_odd_abundant_sieve multiple times, doubling the limit every time, until we have at least 20 results. I wouldn’t bother, though.
You might be wondering, “how does this perform compared to the MPU version?”
For small values (the first 23 numbers in the sequence), the MPU version is faster by about 200%. However, when given more realistic limits, our better algorithm pulls ahead. It breaks even at about 100 numbers on my machine. By the time we ask for 150 numbers, the sieve is already 60% faster.
Benchmarks are an incredibly useful—and essential—tool when you need to write high performance code. Knowing that one algorithm is faster than another doesn’t always translate to real code. When dealing with implementation details, those hidden constants can really make a difference. What’s also really important, however, is knowing your requirements. If we’re only ever going to need to find less than 100 abundant primes, the MPU version might be a worthy choice. However, if we want to push it beyond that, then the better algorithm wins.
Of course, translating the sieve algorithm to tight C code would blow both of them out of the water at any value of n, since the sieve version grows strictly slower than the MPU version.
Raku
Here’s a quick port to Raku. If you’re only concerned with outputting the results, there’s no point in storing them first:
sub MAIN(Int $lim = 10000) {
my @div_sum; # Sum of divisors for each number
for 1...$lim -> $n {
@div_sum[$n*$_] += $n for 1..$lim/$n+1;
$n.say if $n % 2 and 2*$n <= @div_sum[$n];
}
}
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
Task #2 this week is no doubt about first class functions, but gets more specific, asking us to have a go at function composition:
Create sub compose($f, $g) which takes in two parameters $f and $g as subroutine refs and returns subroutine ref i.e. compose($f, $g)->($x) = $f->($g->($x))
Before we get too far ahead of ourselves, let’s briefly review what these terms mean.
First Class Functions
A language that supports first class functions simply allows you to pass functions around like any other variable. Passing anonymous functions (also known as lambda functions) around is usually included in this definition as well. Perl makes this easy:
my $add2 = sub { $_[0] + 2 }; # Returns a sub that adds 2 to its argument
$sub->(5); # Returns 7
That example may not be the most compelling, but for some motivation, look no farther than Perl’s map or grep builtins. When you call something like map { $_ * $_ } 1..10 to get the first ten square numbers, that block { $_ * $_ } is an anonymous subroutine.
First class functions are incredibly useful, and deserve more discussion than I can cram into this blog post, so perhaps I’ll do them justice with a longer dedicated post in the future.
Function Composition
Function composition is a distinct concept in mathematics. In computer science, it depends on first class functions, but is otherwise not related. Function composition, often denoted with the ∘ operator, takes two functions f and g and produces a new function:
\(h = g \circ f \text{ such that } h(x) = g(f(x)) \)
The reason it’s usually written as g ∘ f is that in plain English, g follows f, because we are feeding the output of f into g. Of course, f and g are just symbols, so they can be swapped to match the task description with no issues:
\(h = f \circ g \text{ such that } h(x) = f(g(x)) \)
Perl
Now that we’ve gotten all of the pesky definitions out of the way, the code is … well, there’s hardly any code at all, really. Here’s a function that generates the composition h = f ∘ g:
sub comp {
my ($f, $g) = @_;
sub { $f->($g->(@_)) }
}
Here’s an example usage that calculates the sum of squares of a list of numbers:
use List::Util qw< sum0 >;
my $squares = sub { map { $_ * $_ } @_ };
my $h = comp( \&sum0, $squares );
say "The sum of squares for 1..10 = " . $h->(1..10); # 385
I chose to use List::Util‘s sum0 function so I could demonstrate how to pass in a reference to a named function. The $squares function shows how to use a variable. I could have also done this as an anonymous function:
my $h = comp( \&sum0, sub { $_ * $_ } @_ } );
Raku
Raku’s first class function support is very good. In fact, the language was designed around higher order features like this, so there are some built-in helpers we can use, such as the composition operator. That’s right, we can use ∘ or o right in our code to do the function composition. I could stick this into a comp function like I did with the Perl example, but that seems less expressive to me.
my &sum = sub { [+] @_ };
my &square = sub { @_ »*« @_ };
my &h = &sum ∘ □
say &h(1..10); # 385
First class functions open up endless possibilities in your code.
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
We’re back with our noses to the mathematical grindstone this week, with two straightforward tasks.
Task 1 › Primordial Numbers
The nth primordial number is simply the product of the first n primes. P(1) = 2, P(2) = 2×3 = 6, P(3) = 2x3x5 = 30, etc. P(0) is defined to be 1 as a special case. Since I’ve implemented various prime number generators before, I just went with Math::Prime::Util for this one, making use of the prime_iterator function:
my $it = prime_iterator;
say my $pri = 1; # P(0) = 1 by definition
say $pri *= $it->() for 1..$ARGV[0] // 10;
Easy.
Task 2 › Kronecker Products
I haven’t worked with Kronecker products for quite a few years, so when I reviewed the definition, I thought it might be tricky to implement, so I got a fresh caffeinated beverage, but much to my dismay, it was all over before my second sip.
Please do check that link for a more rigorous definition of Kronecker products. As a quick review, I will simply show an example, with ⨂ as the operator for the Kronecker product:
\(A = \begin{bmatrix}2 & 3 \\ 4 & 5 \end{bmatrix} \\ B = \begin{bmatrix}a & b \\ c & d \end{bmatrix} \)
To make this happen, I opted to loop over the total number of rows in A ⨂B and use division and modulo arithmetic to determine which sub-row and -column in B we need. I use a triple-nested map to achieve the multiplications and orderings of the final matrix.
sub kronecker {
my ($A, $B) = @_;
map {
my $i = $_;
[
map {
my $aval = $_;
map { $aval * $_ } $B->[$i % @$B]->@*;
} $A->[$i / @$B]->@*
]
} 0..(@$A * @$B)-1;
}
The post-deref (->@*) looked a bit cleaner here, so I went with that, but @{$B->[$i % @$B]} would have worked just as well.
The result is a list of array refs containing the rows of the final product. The problem description didn’t specify, but I opted to also include a pretty-print routine to display the output a little nicer than Data::Dump can:
This post is part of a series on Mohammad Anwar’s excellent Weekly Challenge, where hackers submit solutions in Perl, Raku, or any other language, to two different challenges every week. (It’s a lot of fun, if you’re into that sort of thing.)
This week, both tasks are quite short, so I’ll combine them into a single blog post.
Task 1 › Brilliant Numbers
Brilliant numbers are composite numbers with exactly two prime factors. Additionally, the prime factors must be the same length.
